- 作者:Ghassel A, Robinson I, Tanase G, et al.
- 发表单位:Queen’s University, Kingston, Canada;Amazon
- 发表在:第 31 届 SIGKDD 会议(2025)
核心内容
- RAG 只关心语义相似,忽略语义不同的资料的特点一向广为人所诟病,本文提出了层次词汇图(Hierarchical Lexical Graph,HLG)来解决这一问题。
- HLG 可分为三层:
- 溯源:为每个原子命题追溯原文档
- 聚类:为原子命题聚类
- 实体路径:将实体和关系连接起来生成路径
- 在 HLG 基础上,作者提出了两种检索方法:
- StatementGraphRAG:在命题上执行针对实体的集束搜索来应对事实型问题;
- TopicGraphRAG:选取相关主题来获取更多相关上下文信息
- 作者觉得目前的 benchmark 不够好,于是又搭建了一条数据集生成管线制作了一个人造多文档问答数据集;在 5 个数据集上本文的思路可以超越基础的 chunk-based RAG 23 个百分点。
背景
- RAG 使用的向量搜索只能捕捉到 query 和 doc 之间最表层的语义关系,而基于图的检索方案则提供了一个很有潜力的解决思路;
- 搜索 Text Chunk 的方案局限性已经日渐显露,目前的一个趋势是减小搜索单元的大小。比如采用命题来作为基础检索单元来提升检索精确性;
- HLG 则更进一步,采用了包含多种搜索粒度的多层架构:
- Lineage:使用的每个陈述都溯源到源文档
- Summarization:将陈述按照主题聚类来执行更加灵活的搜索
- Entity-Relationship:自底向上的图搜索
- 然后在 HLG 上执行两层搜索:
- StatementGraphRAG:针对命题进行搜索,不同文档中的命题(Summarization)之间通过实体关系(Entity-Relationship)连接起来,并且通过 Lineage 提供溯源;
- TopicGraphRAG:和前者很相似,不过这次针对的是以主题为单位的一簇命题进行搜索;
- 作者用 LLM 基于MultiHop-RAG 语料库制作了一个 674 个问答对。这些问答对经过了 LLM 反复的批评和检查。
提出的方法
HLG
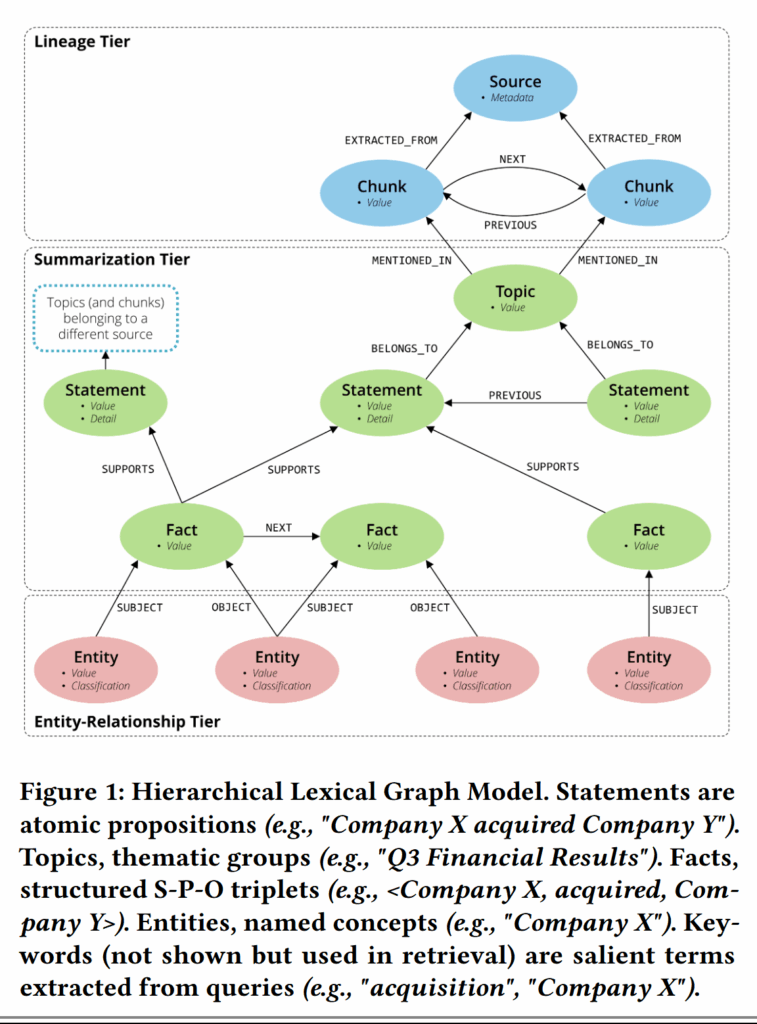
图中有这些结点:
- Lineage:负责溯源
- 元信息:源文档内容描述
- Chunk:文档块内容
- Summarization:检索的核心
- Statement:一段话中的一个完整子句,这是一个原子命题,搜索的主体
- Facts:三元组,包含实体,跨文档的 Statement 靠这个联系起来
- Topic:聚类主题,文档内的 Statement 靠这个联系起来
- Entity-Relationship:负责跨文档(不同文档中提到了相同实体的 Statement 可以被连接起来)
- Entity:Facts 中的主语和宾语
- Relationship:实体间关系
这个图也是单纯用 LLM 生成的,层级连接也是 LLM 识别抽取的。
检索模型
StatementGraphRAG
分为几层搜索:
- 基于关键词搜索:试图通过实体文本匹配检索 statement
- 向量搜索:通过向量匹配 statement 和 query
- 图集束搜索:搜索 HLG 中的多跳邻居,statement 之间是通过共同的 entity 连接起来的;搜索出来的路径会被评分并且排序
- 重排序:重排序路径,获取 topk 结果
设 $\mathcal{G}=(V,E)$ 是 HLG,其中 $\mathcal{S}{\mathcal{G}}\subset V$,是所有 statement 的集合。现在用户提出了 query $Q$,首先提取出一系列关键词: $$ K={ k{i}|k_{i}\text{ was extracted from } Q }
$$
对每个关键词都匹配实体,如果实体出现在了某个 statement $s$ 中,这个关键词就可以被归类到 $K_{s}\in K$。从这里可以获得第一个评分,即 $s$ 能匹配到的关键词数量。这个值越高说明越相关:
$$
\text{Score}{kw}(s)=|K{s}|
$$
从这里,可以取出 topk 相关度最高的 statements 组成 $\mathcal{S}{kw}$: $$ \mathcal{S}{kw}=\text{Top}{k}(\mathcal{S}{\mathcal{G}},\text{Score}_{kw})
$$
然后是向量搜索,取和 $Q$ 相似度最高的一组 statements($\mathbf{e}$ 是编码后的向量):
$$
\mathcal{S}{vss}=\text{Top}{k}(\mathcal{S}{\mathcal{G}}, \text{sim}(\mathbf{e}{s},\mathbf{e}{Q})) $$ 把这两个集合合并起来,我们就得到了一组候选 statements: $$ \mathcal{S}{init}=\mathcal{S}{kw}\cup \mathcal{S}{vss}
$$
前面把 statement 之间的关系定义为了共享实体。那么就沿着共享实体从 $\mathcal{G}$ 中检索出一组路径来。
记路径是一个 statement 序列 $P=s_1, s_2, \dots, s_n$,路径的 Embedding 被定义为序列 statement 语义向量的注意力和(准确来说,是点积注意力,没有缩放):
$$
\mathbf{e}{path}(P)=\sum{i=1}^n\alpha_{i}\mathbf{e}{s{i}},\alpha_{i}=\text{Softmax}(\text{sim}(\mathbf{e}{i},\mathbf{e}{Q}))
$$
同样地,基于这个计算路径相似度评分:
$$
\text{Score}{beam}(P)=\text{sim}(\mathbf{e}{Q},\mathbf{e}{path}(P)) $$ 以 $\mathcal{S}{init}$ 中的 statement 为起点,通过这个评分函数,集束搜索出一组路径。搜索策略是这样的:
- 扩展一个结点之后,路径的评分必须上升,否则停止搜索;
- 抵达最大深度 $D_{\max}$ 后,停止搜索
- 只选择评分最高的 B 个路径继续扩展
最后获得了一组路径。把路径打散,回到一组 statement 的状态 $\mathcal{S}{final}$。最后将所有的 statement 进过 rerank 后选出 topk: $$ \mathcal{S}{top}=\text{Top}{k}(\mathcal{S}{final},\text{Rerank}(Q,s))
$$
写到这里我才意识到,这个检索方法的精度估计大受 rerank 的影响。因为就算通过复杂的图遍历找到了语义上不相似、但是实际上很有用的 statement,rerank 又会按照语义相似度将它排到后面去。
TopicGraphRAG
主要是分为自下而上和自上而下的搜索方法。
- 自上而下:用向量搜索匹配 query 和 topic 结点,找到相似度最高的 topic 以及隶属于 topic 的 statement
- 自底向上:通过 $Q$ 提取的关键词做实体匹配,提到匹配到实体的 statement 会被收集起来
- 图集束搜索 & 重排序:和之前一样,前两步获取的 statement 进行图搜索和重排序
后处理
为了防止太多 statement 撑破 LLM 上下文,作者想了个办法来保持多样性的同时扔掉冗余的 statement。具体来说是用 TF-IDF 权重评价 statement 之间的相似度。相似度过高(高于 0.995)的 statement,保留 rerank 评分最高的那个。
实验
作者在 5 个数据集上进行了实验。
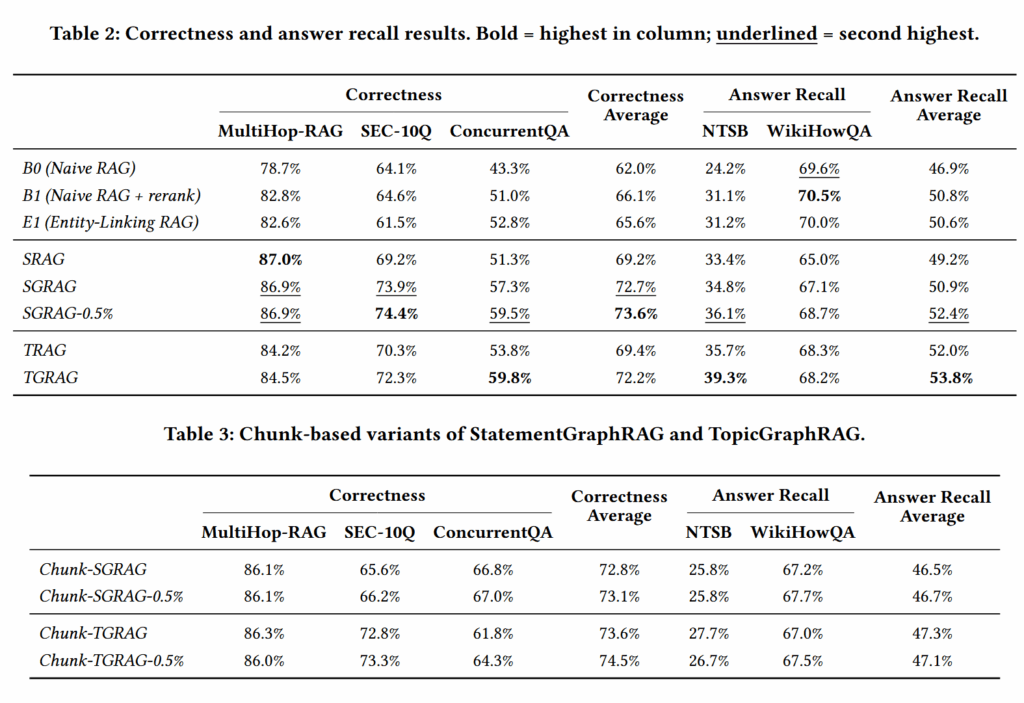
可以发现作者的方案能够超越 Naive RAG+rerank 这样的强基线,而且采用 statement 作为搜索单元确实比使用 chunk 要好。
结论
- 提出了 HLG 这一框架,支持细粒度的多跳检索推理,可以应对复杂的问答任务;
- 实验表明,检索主题或者检索 statement 确实比检索 chunk 要好不少;
- 虽然这个 RAG 的 index 成本很高,但是毕竟是可以预计算,展现出了很好的引用潜力。
启发与评价
- 1.0 技术创新——逻辑思维推理框架:虽然是同期工作,但是这篇文章可以看作是在 PropRAG 的基础上加上了溯源和聚类;其以命题为基本搜索单元以及连接共享实体的命题思路如出一辙,甚至也都使用了集束搜索。作者还做了实验表明命题确实是比 chunk 更好的搜索单元,更适合多跳推理任务;
- 2.1 技术目标——专业手册公众服务:HLG 框架需要耗费较多算力来进行索引,但是一次索引之后就可以多次搜索,总的来说成本低于在搜索过程中多次调用大语言模型的 Agent 方案。不过从实现角度来说,作者最后再次引入 rerank 毫无疑问是会抵消图搜索的作用的(不管是好作用还是坏作用),让整体回到语义匹配的轨道上。而且作者没有做移除 reranker 的消融实验。
- 3.1 场景功能——食养通:这篇文章的结论表明,可以考虑把 rerank 从用于单纯语义匹配扩展到用于评估路径证据,这会比 LLM 成本低得多,也可能更好。