核心内容
- 作者认为,知识图谱三元组是一种过度压缩的知识表示形式,这种过度压缩导致了细节大量丢失,不利于 RAG;
- 于是作者提出一种用命题替代三元组来连接实体的方案,即命题内部的所有实体的关系由命题本身定义;而出现在多个命题之间的实体可以将多个命题之间的实体联系起来;
- 作者提出了一种 PageRank 结合集束搜索的两阶段检索方案来在这样的命题图谱上执行搜索,这个搜索方案是不需要 LLM 参与的;
- 实验表明 PropRAG 在多个数据集上获得了 SOTA 水准。
背景
- 非结构化的 RAG 方法忽略了证据文本之间的联系,导致其在多步推理问题上表现不佳;而结构化的 RAG ,尤其是基于知识图谱的 RAG 又把信息压缩成了三元组,这其中的信息损失太大了。尤其是上下文信息基本上全部丢失了;其他的基于 LLM 的搜索方法又要多次调用 LLM,导致效率十分感人,而且可能存在内部的不一致性;
- 本文的核心洞见:
- 从三元组转向更新的知识表示方法来更好地保存上下文;
- 从隐式的评估每个结点,转向显式、高效地发现推理路径。
- 作者提出了 PropRAG,其:
- 将命题(原子、独立的陈述)替代知识图谱来保存上下文信息;
- 通过基于集束搜索的两阶段检索,发现互联的命题路径并且评分。
方法论
另一种命题图谱
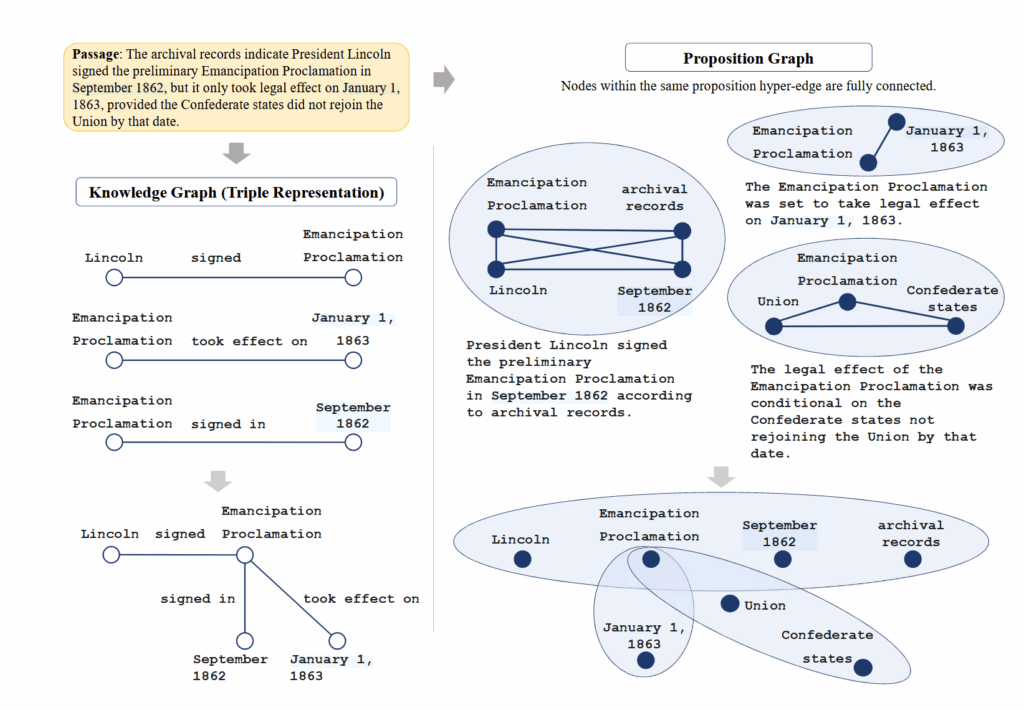
这里的命题是一段独立、原子的并且可能涉及超过两个实体的陈述,如果两个命题涉及相同的实体,就会被认为是连接起来的。比如图中椭圆表示命题,含有相同语义实体的命题会连接起来。
这个命题图谱则是一个用命题连接起来的实体图。命题并非图结点,命题之间只有形式上的联系。相比而言,这篇文章提出的方案经验色彩极重,符合 emnlp 这个会议的名字(自然语言处理的经验方法);而前者则理性色彩偏多。
在这样的命题图谱中,顶点是和知识图谱一样的实体,只有两种边:
- 顶点归属于同一个命题
- 顶点的语义相同(用 embedding 判定)
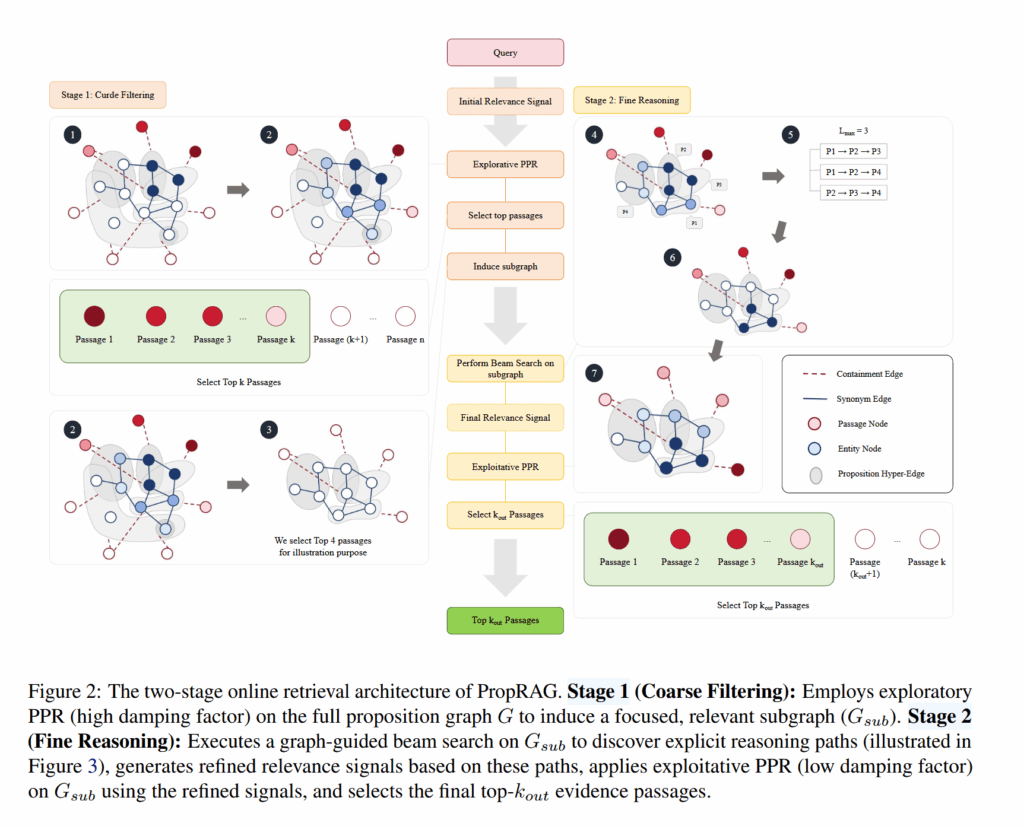
检索流程
给定一个问题 $q$,寻找证据:
- 用 embedding 找出一组和 $q$ 相似度最高的命题 $P_1, P_2, \dots, P_k$
- 命题中的实体被抽取出来,组成了初始种子实体 $S_{initial}=\bigcup_{i=0}^{k}\mathcal{E}(P_{i})$
- 使用 Personalized PageRank 计算实体的权值,PPR 中的初始化集合设为 $S_{initial}$,阻尼系数设为 0.75 来强调联系的作用
- 然后可以计算出每个 passage 的权值(可能是 passage 内所有实体权值的和,没讲),取 topk 之后删去图中 topk 之外 passages 的实体和命题,得到子图 $G_{sub}$
然后就到了第二阶段:
- 对命题执行集束搜索
- 从和 $q$ topk 语义相似的命题开始
- 拓展:提到相同实体的命题被看作相连的,依据这个进行搜索
- 评估:命题路径拼接起来,和问题 $q$ 计算 embedding 相似度,取最高的一组
- 优化过的 $S_{final}$ 集合:包含一开始的 $S_{initial}$ 和集束搜索得出的路径的中心实体(可能是所有实体)
- 用 $S_{final}$ 再来一次 Personalized PageRank,使用更低的阻尼系数 0.45
- 对所有 passage 进行重排序,选取最好的一组作为证据支持 LLM 做出回答
实验
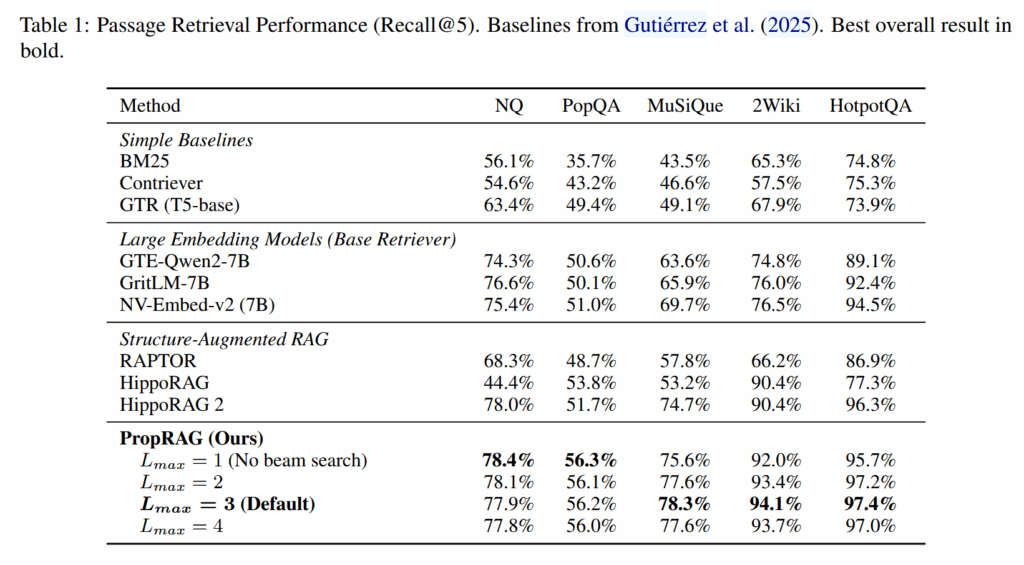
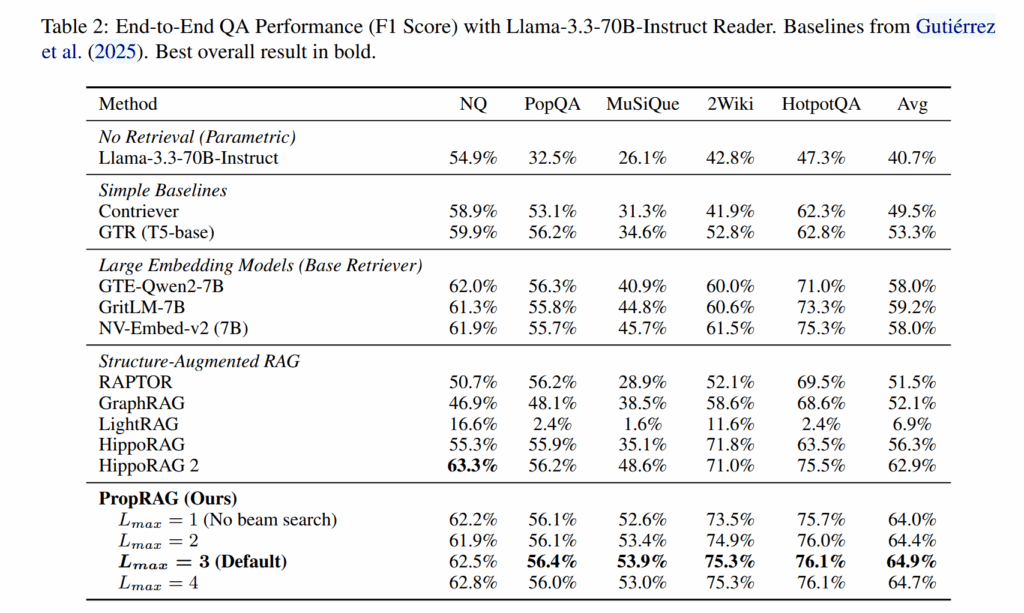
结论
- 这篇文章批判了传统 RAG 以及传统的结构化 RAG 的缺陷,为了解决这些缺陷,他发明了一个命题图谱。一方面命题相同的实体连接起来了,另一方面含有相同实体的命题也连接起来;然后在这上面搜索证据;
- 这篇文章提出了一个基于集束搜索的搜索算法,通过 PageRank 和集束搜索的两阶段检索来筛选出一组 passage 来支持 LLM 回答;搜索方案是完全 LLM-free 的,效率很高;
- 实验证明 PropRAG 在多个数据集上获得了 SOTA 水平
启发与评价
- 作者批判了传统基于三元组的知识图谱在知识表示上存在的缺陷,作者强调三元组是一种过度压缩的信息形式,损失了条件、来源、以及多元关系等关键信息;
- 作者给出的解决方案是通过命题来将实体概念连接起来,同时包含相同实体的命题被看作是相连的,所以这仍然是一种实体图,实体图的边类型是「出现在同命题中」以及「语义相似」;
- 这一种命题图谱可以看作一种用了比三元组更加宽松的形式连接实体的知识图谱,这种更宽松的形式解决了三元组过度压缩的问题;
- 这篇文章提出的是一种文档索引方法,其核心是 PageRank;不过我并不觉得这种命题边组成的图谱服从 PageRank 需要的「链接越多越重要」的假设。并且本文的消融实验没有探究这一点。