- 作者:Yilin Xiao 等
- 单位:香港理工大学(PolyU)
- 发表在:预印本
核心内容
- 问题根源:LLM产生幻觉的根本原因是其学习的是统计学关联而非结构化逻辑,导致生成内容虽流畅但存在事实错误。知识图谱被广泛视为解决此问题的关键方向。
- 研究空白:现有KG-LLMQA方法过度聚焦于证据检索,却忽视了知识间的逻辑关联。复杂推理问题需整合多个独立事实,仅优化检索不足以支撑有效推理。
- 方法创新:提出可靠推理路径(RRP)框架,通过关系嵌入与双向分布学习分别抽取逻辑自洽路径和语义相关路径,并引入反思模块评估路径价值,筛选高质量路径用于答案生成。
- 验证效果:在WebQSP和CWQ等经典KGQA数据集上验证,RRP显著提升性能,且仅需7B参数量的小型模型即可实现优异表现。
背景
- 作者认为,LLM 的幻觉的根源是 LLM 学习到的是统计学上的联系,而非结构化的底层逻辑,因此才会生成包含事实错误、但是语言上又很流畅的答案;在这一思考下,现有的研究往往在思考如何进行知识注入,而知识图谱是一个热门的方向;
- 作者发现,过去大家总在思考如何从知识图谱中检索出更好的证据,但是忽略了知识之间的逻辑关系;由于解决复杂的推理问题必须将多个独立的事实联系起来处理,因此作者认为单纯思考检索的问题那是不够的;
- 作者指出,当前的 KG-LLMQA 有两个难处:知识图谱太过复杂以及现有的方法总是生成大量没什么帮助的推理路径。为了解决这两个问题,作者提出了可靠推理路径(RRP)。RRP 利用关系嵌入和双向分布学习来分别抽取出逻辑自洽路径和语义相关的路径,然后加入一个反思模块来评估每个路径的价值,并且进行筛选;最后筛选得到的路径会被用来生成答案。
- 作者在两个经典的 KGQA 数据集上验证了 RRP 效果,证明 RRP 可以显著提升效果,并且只需要 7B 这样的小型模型。
方法论
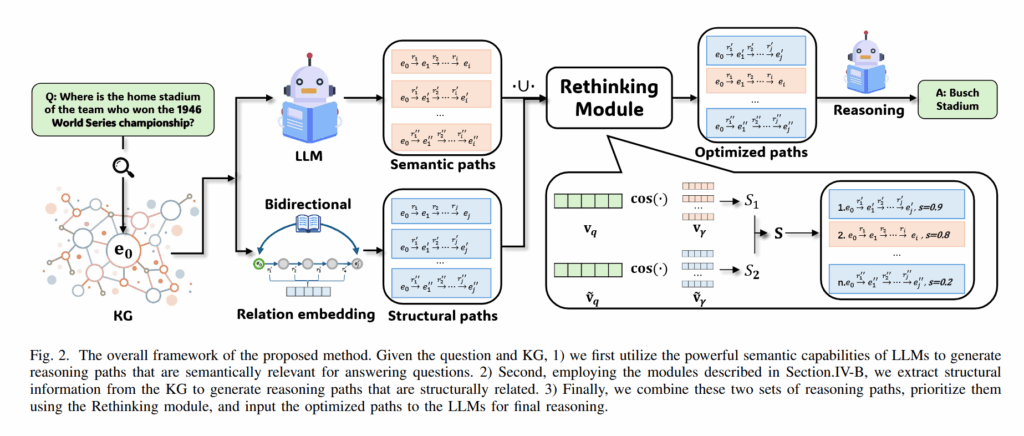
语义推理路径生成
作者希望,LLM 可以根据问题 $q$ 生成直达答案 $a$ 的知识图谱推理路径 $\gamma$。模型可以被表示为先验概率分布 $P_{\alpha}(\gamma|q)$;理想的概率分布则是:
$$
P(\gamma|q,a,\mathcal{G})=\begin{cases}
\frac{1}{\Gamma}, & \exists \gamma(e_{q},e_{a})\in \mathcal{G} \
0, & else
\end{cases}
$$
其中,$\Gamma$ 是从问题实体到答案实体的推理路径集合。作者假定理想的分布是一个均匀分布,如果这样的推理路径在图中存在,那它们有均等的机会出现。
接下来的任务就是想办法近似拟合这一理想分布。对于概率分布来说,我们常常使用 KL散度来衡量概率分布的相似性。因此损失函数:
$$
\mathcal{L}{r{1}}=D_{KL}[P(\gamma|q,a,\mathcal{G})||P_{\alpha}(\gamma|q)]
$$
推导一下:
$$
\begin{array}l
\mathcal{L}{r{1}} & = &\displaystyle \sum_{\gamma \in \Gamma} \frac{1}{\Gamma}[-\log\Gamma-\log P_{\alpha}(\gamma|q)] \
& = & \displaystyle -\frac{1}{\Gamma}\sum_{\gamma \in\Gamma} \log P_{\alpha}(\gamma|q)-\log\Gamma
\end{array}
$$
这个函数它可以求导,求导后常数项就消失了。要使用这个损失函数训练,我们只需要找一组包含问题($q$)、问题实体($e_{q}$)、答案($a$)、答案实体,并且问题实体和答案实体之间的路径($\Gamma$)已知的数据。
模型生成一个序列的概率被看作组成这个序列所有的 token 的生成概率的积。这个积的本质其实是条件概率的链式法则。
结构推理路径生成
这一个步骤更加古典也更加复杂。大致可以分为两个阶段:
- 分析问题:将问题分解为一组知识图谱上的推理步骤;
- 图上搜索:根据推理步骤在图上走出一组路径证据。
分析问题
对于问题 $q$,作者使用了 RNN 思路来将其转换为一组推理步骤。首先用 GloVe 将 $q$ 进行词嵌入:
$$
{ \mathbf{v}{q}^{ini} }=\text{GloVe}(q) $$ 接着,嵌入后的向量使用 RNN 进行编码,编码取最后的隐藏层向量作为 $q$ 的编码向量。这是 encoder 的常见做法: $$ \mathbf{v}{q}=\text{LSTM}({ \mathbf{v}{q}^{ini} }) $$ 然后用一个 LSTM decoder 对其解码,解码为一组向量 ${ \mathbf{w}{i} }^n$,这组向量被视作分析问题得到的解题推理步骤,也就是所谓的导航指令(instruction),被用于指导图上搜索。
图上搜索
一开始,图上所有的关系会被赋予一个可学习的词嵌入向量 $\mathbf{v}{r}$,这个有待训练。我们用关系向量定义实体向量。每个实体向量都是其周围所有关系的加总: $$ \mathbf{v}{e}^{0}=\sigma\left( \sum_{(e,r,e’)\in \mathcal{G}} \mathbf{v}{r}W{1} \right)
$$
头上的 0 表示这是实体向量的初始状态。实体向量会在一轮轮迭代中更新。
对于知识图谱上的每个三元组,我们都根据当前的导航指令 $\mathbf{w}{i}$,编码一个 match 向量: $$ \mathbf{m}{(e,r,e’)}^i=\sigma(\mathbf{w}{i} \odot W{2}\mathbf{v}{r}) $$ match 向量代表这一关系语义上是不是和当前的导航指令相似,接下来会被用于评估从 e 周围的某关系多大程度上是符合导航指令的。然后再将其按权加总,汇集成 e 的信息向量: $$ \tilde{\mathbf{v}}{e}^i=\sum_{(e,r,e’)\in \mathcal{G}}P^{i-1}{e’}\mathbf{m}^{i}{(e,r,e’)}
$$
其中,$P^{i-1}{e’}$ 是一个概率值,表示上一个导航指令中 e’ 多大程度上值得作为下一步选择。最后更新实体向量: $$ \mathbf{v}{e}^{i}=\text{FFN}([\mathbf{v}{e}^{i-1};\tilde{\mathbf{v}}{e}^{i}])
$$
然后再度根据实体向量汇总成的矩阵,用一次变换之后计算出 logit 向量,最后计算出概率:
$$
P^{i}=\text{Softmax}(V^{iT}W)
$$
通过上述步骤,我们针对每一步导航指令,都计算出了一个概率图 $P^{i}$。理论上只要找到第一个问题中的实体 $e_{q}$,然后在 $P^{1}$ 图上找到周围概率最大的邻居,然后走向这个邻居即可。这样 n 轮之后理论上就抵达了终点 $e_{a}$。
理论上,这条路径是可逆的,就是说从 $e_{a}$ 也能用相同的方式在 n 轮之后找到 $e_{q}$。所以作者也另外训练了一套从终点回溯到起点的解码器,力求两个解码器计算出的某一步概率图能够实现第 $i$ 步分布 $P^{i}{f}$ 接近逆向回溯解码得到的第 $n-i$ 步概率分布 $P^{n-i}{b}$。作者使用 KL散度和 JS散度来衡量概率分布的相似性,由此得到损失函数:
$$
\mathcal{L}{r{2}}=D_{KL}(P_{f}^{i}||P_{f}^{})+D_{KL}(P_{b}^{i}||P_{b}^{})+\sum_{i=1}^{n-1} D_{JS}(P_{f}^{i}||P_{b}^{n-i})
$$
其中,$P^*$ 是数据集给出的答案推理路径形成的分布(假设为均匀分布);$D_{JS}$ 用于衡量两个分布之间的理论相似性。
再思考
再思考部分使用两个打分器分别评估路径的语义相似度和结构相似度,然后加权。最后可以得出一个路径的评分,筛去那些不太有用的部分。

实验
经典的 WebQSP 和 CWQ,并且获得了最好的效果:
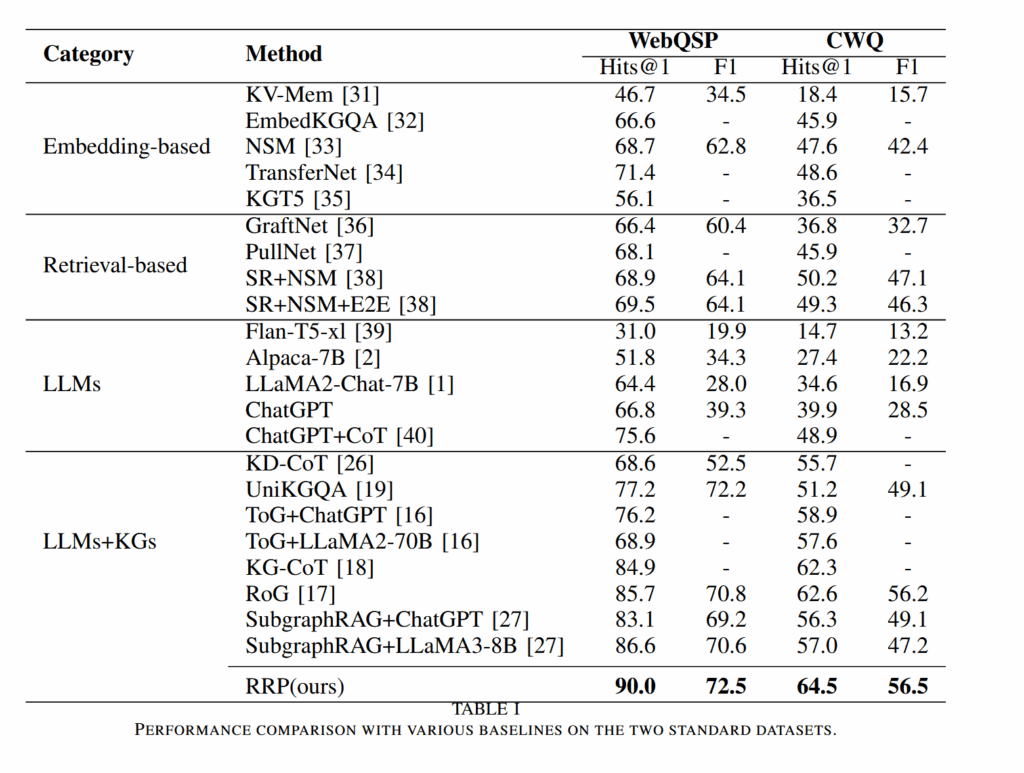
结论
- 提出了 RRP,一个结合了 LLM 的知识图谱增强推理系统。RRP 有效地结合了LLM 的语言能力以及双向学习编码器提供的丰富结构信息,保证了推理的广度和精度,大大提高了推理质量。
- 做了充分的实验对比证明了 RRP 的能力,在多个基准上超越了所有的基线,获得了 SOTA。而且本身 RRP 是一种 plug and play 的框架,可以适用于任何 LLM,减少了迁移到其他问题上所需的工作。
启发与评价
- 作者没有使用单一的 LLM 生成或是 KG-Retrieval,而是结合二者一起来打分,最终筛选出一组干净的证据。这充分结合了二者的优点,实验也可以支持这样的假设;
- 作者在文章中描述方法描述得并不清楚;如果不使用其他技巧的话,这一方法需要围绕知识图谱训练,且需要针对全图实体进行计算。计算量(包括训练)将随着知识图谱的大小线性增加,很难想象作者如何在文章中说的那种具有数千万实体的大型知识图谱上实现这样的训练;
- 作者宣称的 plug-and-play 其实是虚假的。因为 RRP 既需要专门训练的 LLM ,又需要针对具体知识图谱和问题数据集做双向训练,能更换的其实只有回答层的 LLM。将这一方法迁移到其他数据集上的成本是非常高的;
- 没有在任何地方找到源代码,找不到模糊部分的根据。