作者：Yu Zhao,Pan Deng,Junting Liu,Xiaofeng Jia,Jianwei Zhang
单位：北京航空航天大学，北京大数据中心，开普信息股份有限公司
来源：KDD ’23

一、研究背景与意义

现实世界中的复杂系统，如交通系统、大脑、生态系统、社会网络等，支撑着我们理解和分析自然行为的能力。时空数据作为主要表现形式，反映了复杂系统的演化过程。从可观测的时空数据中挖掘隐含的连续时间动力学是理解、预测和控制自然界中复杂系统的重要方法，称为时空表征学习。它在时空序列预测、异常检测和视频分析等多个任务中得到了广泛的研究。

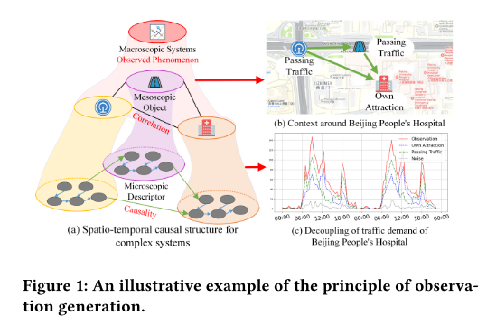
(a):复杂系统可以自然地表示为时空图网络，其中空间节点表示对象或子系统，节点属性表示时间演化过程，而链接表示它们的相互作用。
(b):医院周边的交通需求受到地铁站和主要道路的影响。
(c):北京市人民医院周边交通需求的观察显示，早、中、晚高峰时段明显。
如图中的例子所示，在微观因果描述符的层面进一步分解医院的交通需求，可以发现早晚高峰时段以过往车流为主，而中午高峰时段则由医院本身的吸引力决定。

二、主要贡献

•本文对复杂系统的因果关系进行了自上而下的分析，揭示了观测在微观层面上的生成原理，并系统地定义了由非平稳外生因素调制的因果描述符的时空转换过程。
•本文提出了一个理论基础上的生成性因果解释模型，该模型通过时空因果表征从观测数据和归纳偏差中推断出具有解释能力的微观因果描述符。

三、模型与方法

1、变分自动编码器

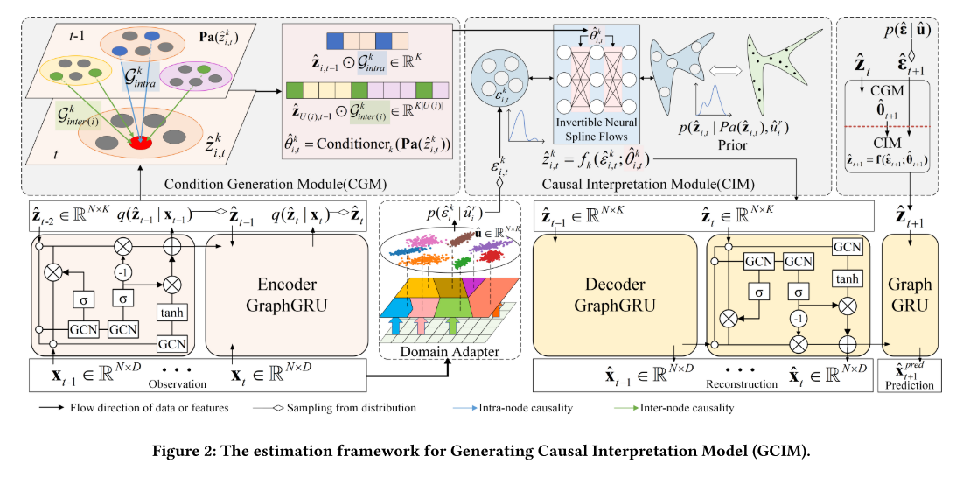
本文利用变分自动编码器框架对推理和生成过程进行建模。如图2所示，GraphGRU用作编码器和解码器，以同时处理空间和时间维度，其定义如下：

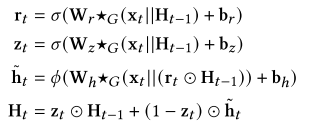
其中||表示级联运算，𝜎表示Sigmoid函数，x𝑡∈R𝑁×𝐷表示观测值，w，b表示图形卷积的参数，G∈R𝑁×𝑁是预定义的区域距离邻接矩阵，𝑁为节点数。

推理阶段的目的是适应𝑔。从观测值x𝑡推断因果描述子的后验分布，这是一个各向同性的高斯分布，其均值和方差来自编码者。生成阶段的目的是拟合𝑔−1。我们以重新参数的方式从后验分布中采样估计的因果描述符𝑡，并使用解码器从估计的因果描述符生成节点观测。

2、域适配器

在大多数情况下，虽然由于域的影响，观测是非平稳的，但是域信息通常是未知的。本文提出了一种域适配器来从观测中捕获潜在的域信息，并使用Gumbel-Softmax技巧来确保每个节点的观测只属于特定的域，定义如下：

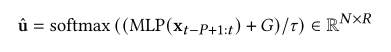
其中mlp是具有泄漏的多层感知器，𝜏是温度变量，𝐺是来自Gumbel(0，1)的I.I.D样本的矢量，x𝑡−𝑙+1：𝑡∈R𝑁×𝑃×𝐷表示时间窗口𝑃内的观测信号。

3、条件生成模块

为了充分捕捉时空因果结构，本文提出了一个条件生成模块(CGM)。本文将时空因果结构分解为节点内因果关系G𝑖𝑛𝑡𝑟𝑎∈{0，1}𝐾×𝐾和节点间因果关系G𝑖𝑛𝑡𝑒𝑟(𝑖)∈{0，1}𝐾×𝐾|𝑈(𝑖)|，并用一个可学习的参数矩阵对它们进行建模。使用Gumbel Softmax来确保G𝑖𝑛𝑡𝑟𝑎和G𝑖𝑛𝑡𝑒𝑟(𝑖)是可以反向传播的离散分布的样本。邻接关系𝑈(𝑖)作为节点间因果关系的归纳偏差，将参数矩阵G(𝑖𝑛𝑡𝑒𝑟(𝑖)从O(𝑁𝐾2)压缩到O(|𝑈(𝑖)|𝐾2)，其中𝑈(𝑖)≪𝑁，大大减少了可学习参数，提高了可识别性。

根据因果描述符的条件无关性，通过条件算子𝑘将时空因果结构得到的母变量转化为转移函数的条件参数：

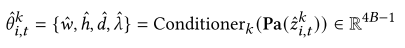
4、因果解释模块

以往的基于变分自动编码器（VAE）的表示学习方法使用标准的多变量高斯先验对潜在变量的后验进行正则化，这极大地限制了模型的表达能力。为此，本文提出了一个因果解释模块，它的目的是基于因果转移函数来模拟因果描述符的先验分布。此外，使用可逆神经样条流来拟合𝑓𝑘。它的具体形式是由来自母变量的条件参数ˆ𝜃𝑘𝑖，𝑡(ˆ𝑧𝑘𝑖，𝑡)调制的，并且这些参数在潜在变量维度上是独立的。

本文使用变量变换公式将先验分布转换为因式分解的外生变量分布，定义如下。

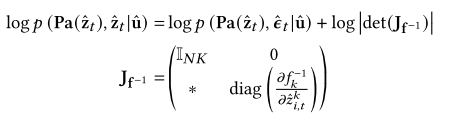
5、预测

基于潜在变量估计的系统未来状态预测是产生式模型的重要能力之一。如图2所示，假设领域在短时间内不变，因此可以从外生变量分布中抽样下一时刻的外生变量。CGM生成转移函数的条件参数。然后，CIM将外生变量转换为因果描述符。最后，解码器生成下一时间的时空序列。预测过程如下：

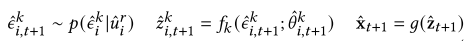
四、实验

1、评估指标

•MCC：标准度量–皮尔逊平均相关系数，在合成数据集上的真实因果描述符和相应的描述符之间计算皮尔逊平均相关系数。为了计算这个性能度量，首先计算真描述符和估计描述符之间的所有相关系数对。然后将每个估计的描述符分配给它最相关的真实描述符，从而匹配表示空间中的任何排列。高MCC意味着真正的描述符被成功识别，直到排列和分量可逆变换。
•RMSE：真实和预测的时空序列之间的均方根误差
•MAE：真实和预测的时空序列之间的平均绝对误差
•MAPE：真实和预测的时空序列之间的平均绝对百分比误差

2、基线模型

非线性ICA方法：
•IVAE：假定潜变量的先验是条件独立的指数分布族。
•Leap：假设潜在变量的先验是一个非参数的时滞因果过程。

时空表示学习方法：
•DGCRN：通过组合预定义的邻接矩阵和输入特征来生成动态图形。
•DMSTGCN：设计了一种自适应图构造方法来学习路段特定时间的空间相关性。
•RGSL：导出了一种稀疏隐式稠密图结构，并融合了显式图和隐式图。
•DSTAGNN：设计了复杂的多头注意和多尺度门控卷积来提取动态时空相关性。
•D2STGNN：分离了扩散和固有的观察特征，并使用自我注意机制来处理长期依赖关系。
•STNSCM：以结构因果模型为基础，通过干预消除混杂因素，并将预测任务视为回答反事实问题。
•CCHMM：利用变分推理将运输系统中的核心物理概念表示为因果隐藏变量。

3、合成数据集实验

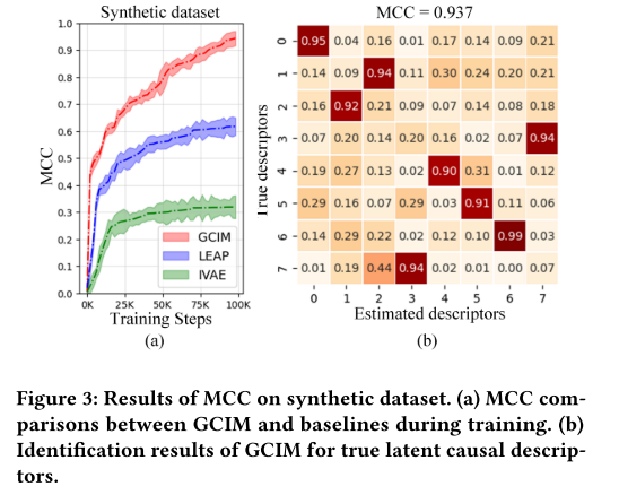
图3显示了合成数据集上GCIM和基线之间的MCC结果。本文的方法成功地识别了潜在的因果描述符，如图3(B)所示，直到排列和分量可逆转换。IVAE没有对时间转换过程进行建模，并且假设潜在变量是独立的分量。IVAE完全忽略了时空因果关系，这使得它几乎无法处理时空数据。LEAP将先验过程建模为非参数、非平稳、时滞的因果过程。然而，由于缺乏对空间维度的考虑，LEAP不能有效地识别时空因果变量。

比较结果充分说明了时空数据中空间因果关系的重要性。GCIM设计了一个可学习的节点间因果关系矩阵来捕捉每个节点局部邻域内的空间因果关系，有效地支持了相邻变量的可识别性。如图4所示，本文在合成数据集上可视化节点内和节点间因果关系矩阵，GCIM能够成功地恢复时空因果关系。

4、真实数据集实验

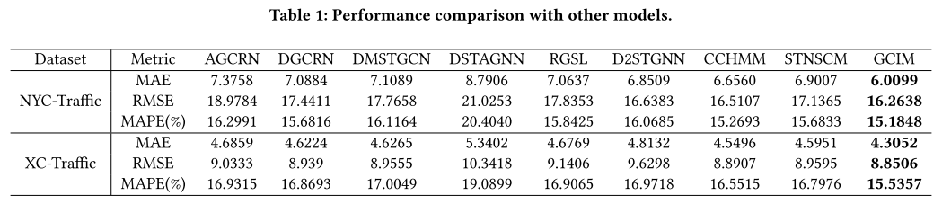
表1给出了三个独立实验的平均结果的总体预测性能。对于时空序列，观测的维度越高，系统内部的因果关系越复杂，MAPE能有效地反映模型抵抗随机波动的能力。因此，我们的GCIM始终以压倒性优势超过基线模型。特别是在多模式交通数据集XC-Traffic上，GCIM在MAPE方面有了显著的改善。

图5显示了本文的模型和测试集上的基线的MAE的演变趋势。得益于对系统内部因果关系的准确建模，本文的模型在每个阶段都表现得最好，这反映了它的稳定性。

5、消融实验

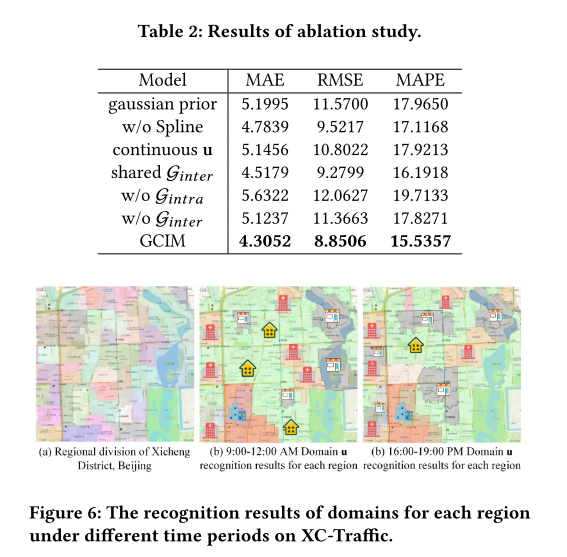
消融实验的性能如表2所示。显然，外部变量的非平稳性是至关重要的。事实上，外生变量只影响系统，而不受系统的约束。这意味着我们只能通过条件信息，即域信息来确定它们。最终，没有条件信息的模型退化为一般的序列表示学习模型。如果域信息是连续变化的随机变量，则域信息连续且轻微地变化，导致域变化的边界丢失，使得不可能确定域中的变化是否大到足以容易识别。

在此基础上，对不同时间段的域名识别结果进行了可视化处理。如图6所示，域适配器成功恢复了不同地域的域信息，尤其是医院属性。医院周边的流量具有鲜明的特点，域适配器可以自动将流量模式相似的区域归入同一类别。此外，不同地区的域名会随着时间的推移动态变化，一些地区会在下班时间显示购物属性。

五、总结

• 传统模型通常依赖动态相关性，这可能会掩盖潜在的因果机制和生成规则。本文使用生成性因果模型来学习、解释和预测复杂的高维时空数据。
• 因果机制和生成规则在不同情况下被认为是稳定和不变的。本文重点在微观层面的潜在因果结构和机制，而不仅仅是动态相关性。
• 本文的生成性因果解释模型（GCIM）从观测数据中推断具有解释能力的微观因果描述符，同时利用了时空因果表示，扩展了变分自编码器（VAE）来估计因果描述符的先验分布。